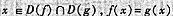题目内容
（请给出正确答案）
[主观题]
设＜ G,*＞是一个群,且a∈G。定义一个映射f:G-＞G,使得对于每一个x∈G,有f(x)=a*x*a-1，试证明f是＜ G,*＞的群自同构。
设＜ G,*＞是一个群,且a∈G。定义一个映射f:G-＞G,使得对于每一个x∈G,有f（x)=a*x*a-1，试证明f是＜ G,*＞的群自同构。
查看答案
如果结果不匹配，请 联系老师 获取答案
题目内容
（请给出正确答案）
如果结果不匹配，请 联系老师 获取答案
题目内容
（请给出正确答案）
如果结果不匹配，请 联系老师 获取答案
更多“设＜ G,*＞是一个群,且a∈G。定义一个映射f:G-＞G,…”相关的问题
设G是一个群，a∈G。映射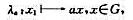
叫做G的一个左平移。证明：
(i)左平移是G到自身的一个双射;
(ii)设a，b∈G，定义λaλb=λa·λb(映射的合成)，则G的全体左平移{λa|a∈G}对于这样定义的乘法作成一个群G';
(iii)G≌G'。
设＜G,+＞是Abel群,EndG是G的所有自同态的集合，
f,g∈EndG定义+和○运算:a∈G,
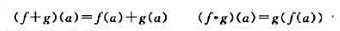
证明EndG关于+和○构成一个环.
设G与G'都是群，f是群G到G'的同态映射,a∈G.
(1)证明若a的阶是有限的,则f(a)的阶也是有限的，且|f(a)|、整除|a|.
(2)如果f(a)的阶是有限的，那么a的阶一定是有限的吗？证明你的结论.
设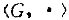
是一个群、对于a,b∈G,若a·b=b·a,a和b的阶分别是r和s,且循环子群(a)和(b)的交只包含G的么元e,则a·b的阶等于r和s的最小公倍数。
设f为一函数,g为一函数,求证:
(1)f∩g是以D(f∩g)为定义域的一个函数
(2)fUg是以D(fUg)为定义域的函数当且仅当对每一
证明G是交换群
证＜ H,*＞是正规子群。
