 更多“设G为群,且存在a∈G,使得证明G是交换群”相关的问题
更多“设G为群,且存在a∈G,使得证明G是交换群”相关的问题
第1题
设< G,*>是一个群,且a∈G。定义一个映射f:G->G,使得对于每一个x∈G,有f(x)=a*x*a-1,试证明f是< G,*>的群自同构。
设< G,*>是一个群,且a∈G。定义一个映射f:G->G,使得对于每一个x∈G,有f(x)=a*x*a-1,试证明f是< G,*>的群自同构。
点击查看答案
第2题
设f(x),g(x)∈C[a,b],在(a,b)内可导,且gˈ(x)≠0,证明:存在ξ∈(a,b),使得
设f(x),g(x)∈C[a,b],在(a,b)内可导,且gˈ(x)≠0,证明:存在ξ∈(a,b),使得
点击查看答案
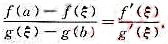
第7题
证明:定理6.6中,,情形时的罗比达法则.(I)(ii)存在Mo>0,使得f与g在(Mo,+∞)内可导,且g'(x)≠0
证明:定理6.6中,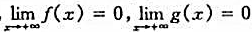 ,情形时的罗比达法则.
,情形时的罗比达法则.
(I)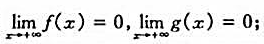
(ii)存在Mo>0,使得f与g在(Mo,+∞)内可导,且g'(x)≠0;
(iii)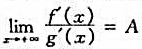 (A为实数,也可为±∞或∞)则
(A为实数,也可为±∞或∞)则
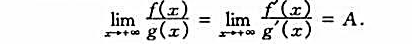
第8题
设A为秩为r的m×n矩阵。证明:存在秩为r的m×r矩阵G和秩为r的r×n矩阵H,使得A=GH(矩阵的这种分解通常称为满秩分解)。
设A为秩为r的m×n矩阵。证明:存在秩为r的m×r矩阵G和秩为r的r×n矩阵H,使得A=GH(矩阵的这种分解通常称为满秩分解)。
点击查看答案
第9题
证明:设uj是有向网络G中自点1到点j的最短有向路的长度,且对所有的j=2,3,...,n,uj为有
限值,若网络G中的点能编成如下的序号2,3,...,n,使得若i<j,有ui≤uj且wji≥0,但等号不同时成立或者ui>uj且wji=+∞,即(j,i)∉A,则方程(6.1)可化简为方程(6.2)。
点击查看答案
第10题
设G与G'都是群,f是群G到G'的同态映射,a∈G.(1)证明若a的阶是有限的,则f(a)的阶也是有
设G与G'都是群,f是群G到G'的同态映射,a∈G.(1)证明若a的阶是有限的,则f(a)的阶也是有
点击查看答案
设G与G'都是群,f是群G到G'的同态映射,a∈G.
(1)证明若a的阶是有限的,则f(a)的阶也是有限的,且|f(a)|、整除|a|.
(2)如果f(a)的阶是有限的,那么a的阶一定是有限的吗?证明你的结论.

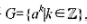 证明G是交换群
证明G是交换群
 如果结果不匹配,请
如果结果不匹配,请 

















