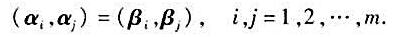题目内容
(请给出正确答案)
题目内容
(请给出正确答案)
n维欧氏空间V的一个线性变换σ说是反对称的,如果对于任意向量a,β∈V。证明:(i)反对称变换关于V的
n维欧氏空间V的一个线性变换σ说是反对称的,如果对于任意向量a,β∈V。
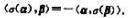 证明:
证明:
(i)反对称变换关于V的任意规范正交基的矩阵都是反对称的实矩阵(满足条件AT=-A的矩阵叫作反对称矩阵);
(ii)反之,如果线性变换σ关于V的某一规范正交基的矩阵是反对称的,那么σ一定是反对称线性变换;
(iii)反对称实矩阵的特征根或都是零,或者是纯虚数。
 如果结果不匹配,请 联系老师 获取答案
如果结果不匹配,请 联系老师 获取答案


 更多“n维欧氏空间V的一个线性变换σ说是反对称的,如果对于任意向量…”相关的问题
更多“n维欧氏空间V的一个线性变换σ说是反对称的,如果对于任意向量…”相关的问题
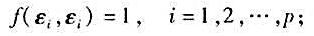
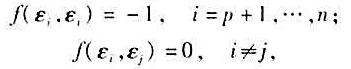
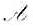 满足
满足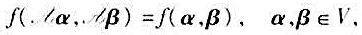
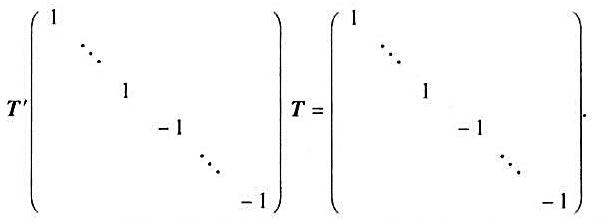
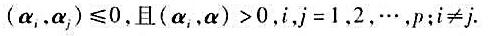
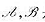 是V的线性变换,且
是V的线性变换,且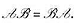 证明:
证明: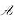 的一特征值,那么
的一特征值,那么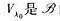 的不变子空间;
的不变子空间;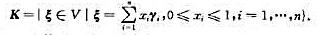
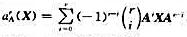 ,r是非负整数,由此推出,如果A是幂零矩阵,那么αA是V的幂零变换;
,r是非负整数,由此推出,如果A是幂零矩阵,那么αA是V的幂零变换;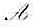 使
使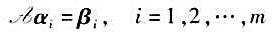 的充分必要条件为
的充分必要条件为