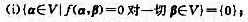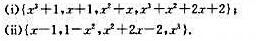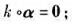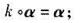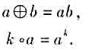题目内容
（请给出正确答案）
令V是实数域R上一个三维向量空间，σ是V的一个线性变换。它关于V的某一个基的矩阵是
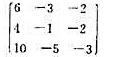
(i)求出σ的最小多项式p(x)，并把p(x)在R[x]内分解为两个最高次项系数是1的不可约多项式p1(x)与p2(x)的乘积;
(ii)令Wi={ξ∈V|pi(σ)ξ=0}，i=1，2。证明，Wi是σ的不变子空间，并且V=W1⊕W2;
(iii)在每一子空间Wi中选取一个基，凑成V的一个基，使得σ关于这个基的矩阵里只出现三个非零元素。
如果结果不匹配，请 联系老师 获取答案
更多“令V是实数域R上一个三维向量空间，σ是V的一个线性变换。它关…”相关的问题
令V=Mn(C)是复数域上全体n阶矩阵所组成的n2维向量空间，令A是任意一个n阶复矩阵。如下地定义V的一个线性变换αA：V→V：对于任意X∈V=Mn(C)，αA(X)=AX-AX。
(i)证明
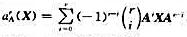，r是非负整数，由此推出，如果A是幂零矩阵，那么αA是V的幂零变换;
(ii)如果A=D+N是A的若尔当分解，其中D是A的可对角化部分，N是幂零部分，那么αD和αN分别是线性变换αA的若尔当分解。
设V是数域F上一个有限维内积空间，配备了一个内积f，证明以下两条件等价：
(ii)f关于V的任意基的格拉姆矩阵非奇异。
满足上述条件的内积叫作非退化的。
检验以下集合对于所指的线性运算是否构成实数域上的线性空间：
1)次数等于n(n≥1)的实系数多项式的全体，对于多项式的加法和数量乘法;
2)设A是一个nxn实矩阵，A的实系数多项式f(A)的全体，对于矩阵的加法和数量乘法;
3)全体n级实对称(反称，上三角形)矩阵，对于矩阵的加法和数量乘法;
4)平面上不平行于某一向量的全部向量所成的集合，对于向量的加法和数量乘法;
5)全体实数的二元数列，对于下面定义的运算：
6)平面上全体向量，对于通常的加法和如下定义的数量乘法：
7)集合与加法同6)，数量乘法定义为
8)全体正实数R+，加法与数量乘法定义为
