题目内容
（请给出正确答案）
设函数f(x)在[1,+∞]上连续、若由曲线y=f(x)与直线x=1,x=t(t＞1)及Ox轴围成平面图形绕Ox轴旋转一周所成的旋转体的体积为
![设函数f（x)在[1,+∞]上连续、若由曲线y=f（x)与直线x=1,x=t（t＞1)及Ox轴围成平](https://img2.soutiyun.com/ask/2020-12-13/976735651562463.png)
试求y=f(x)所满足的微分方程,并求该微分方程满足条件y(1)=2的解.
如果结果不匹配，请 联系老师 获取答案
更多“设函数f（x)在[1,+∞]上连续、若由曲线y=f（x)与直…”相关的问题
设函数y=f(x)在(1，+∞)上连续，若曲线y=f(x)，直线x=1，x=(＞1)与x轴所围成的图形绕x轴旋转一周而成的旋转体体积为
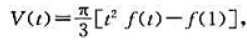
又知道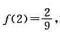
求f(x)。
设函数f(x)在[0,1]上有连续二阶导数f"(x).若f(0)=f(1)=0,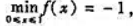
,证明:
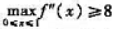
设函数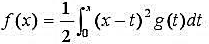
,其中函数g(x)在(-∞,+∞)上连续,且
g(1)=5,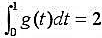
,证明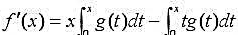
,并计算f''(1)和F'''(1).
设函数f(x)连续,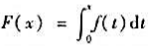
试证:
(1)若f(x)是奇函数,则F(x)是偶函数;
(2)若f(x)是偶函数,则F(x)是奇函数.
设f是定义在R上函数,且对任何x1,x2∈R,都有
若f'(0)=1,证明对任何x∈R,都有
证明反常积分中柯西判别法的极限形式:
(1)设函数f(x)在区间(a,b]上连续(a是奇点).
若有某个正数μ＜1,使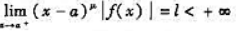
则
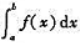收敛.
若有某个正数μ≥1,使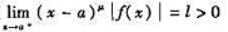
(包括l=+∞),则
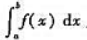发散.
