 题目内容
(请给出正确答案)
题目内容
(请给出正确答案)
问题描述:试设计一个用队列式分支限界法搜索一般解空间的函数,其参数包括结点可行性削定函数
印制电路板将布线区域划分成n×m个方格阵列(见图6-3(a).精确的电路布线问题要求确定连接方格a的中点到方格b的中点的最短布线方案.在布线时,电路只能沿直线或直角布线(见图6-3(b).为了避免线路相交,已布线了的方格做了封锁标记,其他线路不允许穿过被封锁的方格.
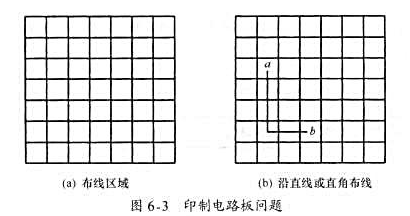
算法设计:对于给定的布线区域,计算最短布线方案.
数据输入:由文件input.txt给出输入数据.第1行有3个正整数n、m.k,分别表示布线区域方格阵列的行数、列数和封闭的方格数.接下来的k行中,每行2个正整数,表示被封闭的方格所在的行号和列号.最后的2行,每行也有2个正整数,分别表示开始布线的方格(p,q)和结束布线的方格(r,s).
结果输出:将计算的最短布线长度和最短布线方案输出到文件output.txt.文件的第1行是最短布线长度.从第2行起,每行2个正整数,表示布线经过的方格坐标.如果无法布线,则输出“NoSolution!".

 如果结果不匹配,请 联系老师 获取答案
如果结果不匹配,请 联系老师 获取答案


 更多“问题描述:试设计一个用队列式分支限界法搜索一般解空间的函数,…”相关的问题
更多“问题描述:试设计一个用队列式分支限界法搜索一般解空间的函数,…”相关的问题
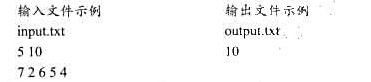
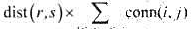 .试设计一个优先队列式分支限界法,找出所给n个元件的布线成本最小的布线方案.
.试设计一个优先队列式分支限界法,找出所给n个元件的布线成本最小的布线方案.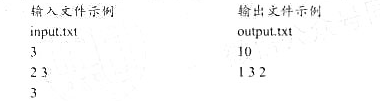

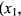 ,
,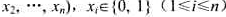 使得
使得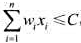 ,而且
,而且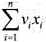 达到最大.因此,0-1背包问题是一个特殊的整数规划问题.
达到最大.因此,0-1背包问题是一个特殊的整数规划问题.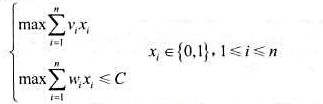

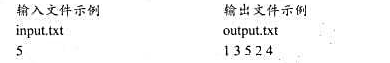
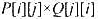 .设计一个算法,计算男女运动员最佳配对法,使各组男女双方竞赛优势的总和达到最大.
.设计一个算法,计算男女运动员最佳配对法,使各组男女双方竞赛优势的总和达到最大.
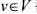 都有权值w(v).如果
都有权值w(v).如果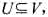 ,且对任意(u,V)∈E有u∈U或v∈U,就称U为图G的一个顶点覆盖.G的最小权顶点覆盖是指G中所含顶点权之和最小的顶点覆盖.
,且对任意(u,V)∈E有u∈U或v∈U,就称U为图G的一个顶点覆盖.G的最小权顶点覆盖是指G中所含顶点权之和最小的顶点覆盖.

















